정렬
1. 선택 정렬
- 주어진 리스트 중에서 최솟값을 찾는다.
- 그 값을 맨 앞에 위치한 값과 교체
arr 배열이 아래와 같을 때,
| 5 | 3 | 1 | 4 | 2 |
↑
최솟값 탐색 : 1
첫 번째 값 5와 최솟값 1을 교환
1회전 결과
| 1 | 3 | 5 | 4 | 2 |
↑
최솟값 탐색 : 2
두 번째 값 3과 최솟값 2를 교환
2회전 결과
| 1 | 2 | 5 | 4 | 3 |
↑
최솟값 탐색 : 3
세 번째 값 5와 최솟값 3을 교환
3회전 결과
| 1 | 2 | 3 | 4 | 5 |
↑
4보다 작은 최솟값이 없으므로 종료
오름차순 완성상태
| 1 | 2 | 3 | 4 | 5 |
for(int i=0; i<n-1; i++) {
for(int j=i+1; j<n; j++) {
if(arr[i] > arr[j]) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
}
2. 삽입 정렬
- 두 번째 자료부터 시작하여 그 앞의 자료들과 비교
- 삽입할 위치를 지정한 후 자료를 뒤로 옮기고 지정한 자리에 자료를 삽입하여 정렬
arr 배열이 아래와 같을 때,
| 5 | 3 | 1 | 4 | 2 |
↑
key : 3
첫 번째 값 5와 비교
| 3 | 5 | 1 | 4 | 2 |
5를 한 칸 뒤로 이동
key 값 3을 첫 번째 자리에 넣음
1회전 결과
| 3 | 5 | 1 | 4 | 2 |
↑
key : 1
두 번째 값 5와 비교
| 3 | 5 | 5 | 4 | 2 |
5를 한 칸 뒤로 이동
첫 번째 값 3과 비교
| 1 | 3 | 5 | 4 | 2 |
3을 한 칸 뒤로 이동
key값 1을 첫 번째 자리에 넣음
2회전 결과
| 1 | 3 | 5 | 4 | 2 |
↑
key : 4
세 번째 값 5와 비교
| 1 | 3 | 5 | 5 | 2 |
5를 한 칸 뒤로 이동
두 번째 값 3과 비교
| 1 | 3 | 4 | 5 | 2 |
3은 그대로 두고
key값 4를 세 번째 자리에 넣음
3회전 결과
| 1 | 3 | 4 | 5 | 2 |
↑
key : 2
네 번째 값 5와 비교
| 1 | 3 | 4 | 5 | 5 |
5를 한 칸 뒤로 이동
세 번째 값 4와 비교
| 1 | 3 | 4 | 4 | 5 |
4를 한 칸 뒤로 이동
두 번째 값 3과 비교
| 1 | 3 | 3 | 4 | 5 |
3을 한 칸 뒤로 이동
첫 번째 값 1과 비교
| 1 | 2 | 3 | 4 | 5 |
1은 그대로 두고
key값 2를 두 번째 자리에 넣음
4회전 결과
| 1 | 2 | 3 | 4 | 5 |
오름차순 완성상태
| 1 | 2 | 3 | 4 | 5 |
for(int i=1; i<n; i++){
key = arr[i];
for(int j=i-1; j>=0 && arr[j] > key; j--){
arr[j+1] = arr[j];
}
arr[j+1] = key;
}
3. 퀵 정렬
- 피벗을 기준으로 피벗보다 작은 요소들은 피벗의 왼쪽에 위치시키고 피벗보다 큰 요소는 오른쪽에 위치시킨다.
- 피벗을 제외한 왼쪽 리스트와 오른쪽 리스트 각각을 다시 정렬한다.
- 분할된 서브 리스트에 대해서는 순환 호출을 이용하여 정렬을 반복한다.
- 서브 리스트에서도 재차 피벗을 정하고 이를 기준으로 2개의 서브 리스트로 다시 나누어 주는 과정을 반복한다.
- 부분 리스트들이 더 이상 분할이 불가능할 때까지 반복한다.
- 리스트의 크기가 0이나 1이 될 때까지 반복한다.
- 분할 (Divide) : 입력 배열을 피벗을 기준으로 비균등하게 2개의 서브 리스트로 분할
- 정복 (Conquer) : 서브 리스트를 정렬한다. 서브 리스트의 크기가 조금 크다고 생각이 들면 재귀 호출을 이용하여 다시 분할 정복 방법을 적용
- 결합 (Combine) : 정렬된 부분 배열들을 하나의 배열에 합병한다.
1. pivot 값을 먼저 정해준다.
- pivot 값은 리스트의 맨 앞, 맨 뒤, 중간 어느 원소로 잡아도 되지만 나는 중간 인덱스로 하겠다.
| 3 | 4 | 1 | 5 | 7 | 2 | 6 |
↑ pivot
2. pivot값을 기준으로 원소들을 재배치한다.
| 3 | 4 | 1 | 5 | 7 | 2 | 6 |
| 3 | 4 | 1 | 2 | 5 | 7 | 6 |
← pivot보다 작은 값 → ← pivot보다 큰 값→
그 결과 pivot 값을 중심으로 두 개의 서브 리스트가 생긴다.
3. 이 서브 리스트들에서 각각 pivot 값을 다시 정해준다.
| 3 | 4 | 1 | 2 | 5 | 7 | 6 |
↑ pivot ↑ pivot
↓
| 1 | 4 | 3 | 2 | 5 | 6 | 7 |
4. 다시 이 pivot 값을 중심으로 대소 비교를 통한 재배치 과정을 진행한다.
- 여기서 오른쪽의 서브리스트는 원소의 갯수가 하나만 남았기 때문에 더 이상 분할 할 수 가 없으므로 오른쪽의 퀵 정렬은 종료
| 1 | 4 | 3 | 2 | 5 | 6 | 7 |
↑ pivot
↓
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
pivot 값을 기준으로 재배치하여 분할을 진행
분할을 통해 나온 양쪽 서브리스트 원소의 갯수가 1개씩만 남았으므로 퀵 정렬이 완전히 종료
오름차순 완성상태
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
void sort(int[] arr) {
quickSort(arr, 0, arr.length-1);
}
void quickSort(int[] arr, int low, int high) {
if(low >= high) { // 종료조건
return;
}
int pivot = low + (high-low) / 2;
int pivotValue = arr[pivot];
int left= low;
int right= high;
while(left <= right) {
while(arr[left] < pivotValue){
left++;
}
while(arr[right]> pivotValue){
right--;
}
if(lefht<=right){
int temp=arr[right];
arr[right]=arr[left];
arr[left]=temp;
left++;
right--;
}
quickSort(arr,low,pivot-1);
quickSort(arr,pivot+1;high);
}
}
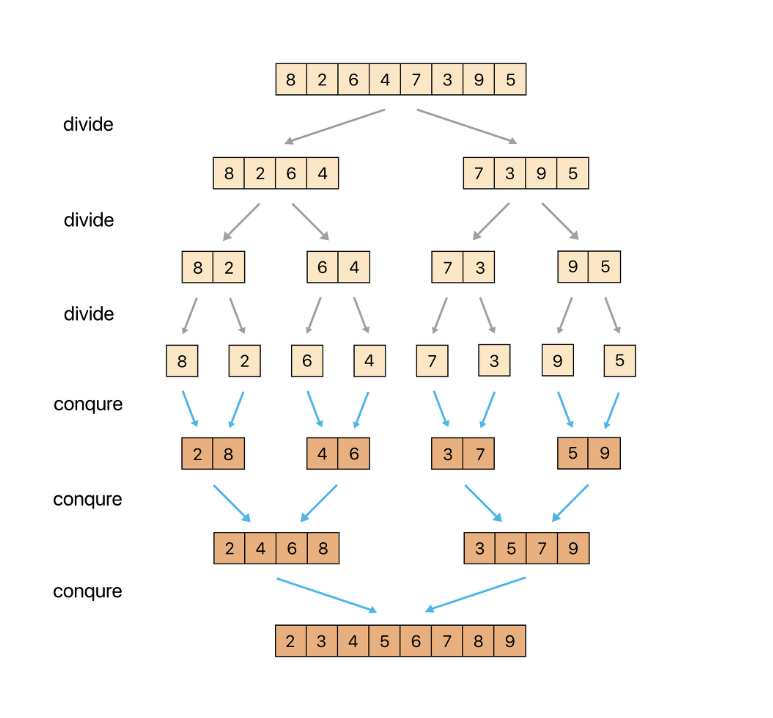
4. 합병/병합 정렬
- 주어진 리스트를 절반으로 분할하여 부분리스트로 나눈다.
- 해당 부분 리스트의 길이가 1이 아니라면 1번 과정을 되풀이한다.
- 인접한 부분 리스트끼리 정렬하여 합친다.
public class Main {
public static int[] src;
public static int[] tmp;
public static void main(String[] args) {
src = new int[]{1, 9, 8, 5, 4, 2, 3, 7, 6};
tmp = new int[src.length];
printArray(src);
mergeSort(0, src.length-1);
printArray(src);
}
public static void mergeSort(int start, int end) {
if (start<end) {
int mid = (start+end) / 2;
mergeSort(start, mid);
mergeSort(mid+1, end);
int p = start;
int q = mid + 1;
int idx = p;
while (p<=mid || q<=end) {
if (q>end || (p<=mid && src[p]<src[q])) {
tmp[idx++] = src[p++];
} else {
tmp[idx++] = src[q++];
}
}
for (int i=start;i<=end;i++) {
src[i]=tmp[i];
}
}
}
public static void printArray(int[] a) {
for (int i=0;i<a.length;i++)
System.out.print(a[i]+" ");
System.out.println();
}
}
5. 힙 정렬
힙 정렬을 알아보기 전에 먼저 힙이 무엇인지 알아야 한다. 그러기 위해선 이진 트리에 대해 알아보자.
이진 트리란 모든 노드의 자식 노드가 2개 이하인 노드를 말한다.

완전 이진 트리는 루트 노드부터 시작해서 자식 노드가 왼쪽 자식 노드, 오른쪽 자식 노드로 차근차근 들어가는 구조의 이진 트리이다. 즉 완전 이직 트리는 이진 트리의 노드가 중간에 비어있지 않고 빽빽히 가득 찬 구조이다.
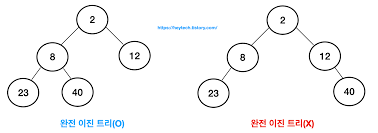
이제 힙에 대해 알아보면, 힙은 최솟값이나 최댓값을 빠르게 찾아내기 위해 완전 이진 트리를 기반으로 하는 트리이다
힙에는 최대 힙과 최소 힙이 존재하는데 최대 힙은 '부모노드'가 '자식 노드' 보다 큰 힙 이라고 할 수 있다.
힙 정렬을 하기 위해서는 정해진 데이터를 힙 구조를 가지도록 만들어야 한다.
이를 위해 힙 생성 알고리즘(Heapify Algorithm)을 사용한다. 힙 생성 알고리즘은 특정한 하나의 노드에 대해서 수행하는 것이다. 또한, 해당 하나의 노드를 제외하고는 최대 힙이 구성되어 있는 상태라고 가정을 한다는 특징이 있다.
힙 생성 알고리즘은 특정한 노드의 두 자식 중에서 더 큰 자식과 자신의 위치를 바꾸는 알고리즘이다. 또한, 위치를 바꾼 뒤에도 여전히 자식이 존재하는 경우 또 자식 중에서 더 큰 자식과 자신의 위치를 바꾸어야 한다.

위와 같이 힙 생성 알고리즘을 통해 힙 구조를 만들었다면 이제 힙 정렬을 시작한다.
1. 루트에 있는 값을 가장 뒤 쪽으로 보낸다.
2. 힙 트리의 크기를 1 줄이고 다시 힙 생성 알고리즘을 통해 힙 구조를 만든다.
위의 과정을 반복하면 정렬이 이루어진다.
int number=9;
int heap[9]={7,6,5,8,3,5,9,1,6};
int main(void){
//힙 구성
for(int i=1;i<number;i+){
int c=i;
do{
int root=(c-1)/2;
if(heap[root]<heap[c]){
int temp=heap[root];
heap[root]=heap[c];
heap[c]=temp;
}
c=root;
} while(c!=0);
}
//크기를 줄여가며 반복적으로 힙을 구성
for(int i=number-1; i>=0; i--){
int temp=heap[0];
heap[0]=heap[i];
heap[i]=temp;
int root=0;
int c=1;
do{
c=2*root+1;
//자식 중에서 더 큰 값 찾기
if(c<i-1 && heap[c]<heap[c+1]{
c++;
}
//루트보다 자식이 크다면 교환
if(c<i && heap[root]<heap[c]{
temp=heap[root];
heap[root]=heap[c];
heap[c]=temp;
}
root=c;
} while(c<i);
}
//결과 출력
for(int i=0;i<number;i++){
printf("%d ",heap[i]);
}
}